Panel Recursive Optimization

I continued the research of the fastest algorithm and I tried to apply a simple recursion instead of an iterative approach; I introduced also another constrain, I wanted to preserve the original vertex normals (each new vertex is obtained by pushing/pulling the original vertex along its surface normal).

The output is a flat panel made out of 4 vertices when it is possible, otherwise there is a compensation made of triangles, still flat of course so it is a combination of quad and tri shapes.

This 9x9 grid, took a little less than 10 seconds to complete.

Panels Optimization with Dynamo

These days I've been giving a Dynamo workshop to Jan, a former Grasshopper user with a big passion for optimization problems and automation.

He showed me a couple of examples were GH is used to solve panels optimization, in particular something that would produce flat panels over an organic surface.

I liked the challenge and we started to discuss possible algorithms to find a Dynamo solution to the same problem.

Firstly the subdivision of the surface only using Dynamo Out Of The Box nodes as opposed to the possibility of using LunchBox (I'd say just for academic purposes), so to have set of points to place adaptive components.

In Revit is relatively easy to get flat adaptive components out of 4 points and Zach Krone showed how to do that in his blog, what you have in return though is a set of panels that are discontinuous, in other words you have gaps along the sides of the panels and usually when I show this example I use a report parameter to measure how much the panels are deviating from the original surface.

The optimization problem is different, basically you accept to have points that are not sitting on the original surface but that are derived from it and that put together will generate a set of flat panels with no gaps, so that the outcome will look like a continuous quad mesh.

I started to think at this problem having in mind the iterative approach that I've seen in the videos that Jan showed me, I came up with a couple of different solutions, each vertex can be further adjusted at each iteration based on a variable number of "target" optimized positions (from 0 to 4) depending on where it is in the grid. If you set an high enough number of iterations you eventually get what you are looking for, but I guess that the optimization should be also after the minimum number of iterations required to get all the panels to be flat.

In the first attempt I've used an iterative approach that took in consideration all the vertices at each cycle, so it was running on a new set of points at each iteration.

In the second attempt I decided to introduce a maximum deviation from the flat condition for groups of 4 points. Basically if 4 points satisfy the maximum deviation condition they are not going to change in the following iterations.

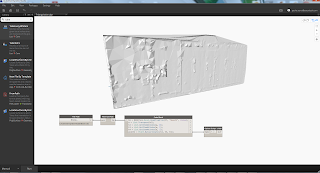
In the image above, on the left you see an output for 5000 iterations over a 9x9 grid generated from the free form surface in Revit on the right.

The grey panels are flat, the colored panels didn't meet the maximum deviation condition (in this particular case it means that the red corners for each panel are more than 0.00001 mm away from the plane that best fit the 4 corners).

In the output I have a value that tells me the number of iterations required and the time elapsed to find the optimized vertices, if the number of iterations reaches the maximum values it means that not all the panels meet the maximum deviation condition.

This kind of processes can bring down the fabrication costs quite sensibly, once again Dynamo saved the day.

Egress Path and Minimum Travel Distance with Dynamo

Yesterday I've been playing with Dynamo to calculate the minimum travel distance and the egress path length for each room of a level in Revit, it is still a work in progress and there is much to do in terms of handling exceptions, avoiding obstacles, but the core is there and it hasn't been that difficult to achieve after all.

I can say that having the possibility to choose among several tools to solve this kind of problems is a very good sensation, I can see several applications for that, in the design phase of course but also in the O&M of a facility, especially when there is valuable equipment that has been moved from one room to another.

I'd like to hear some feedbacks on this so feel free to leave a comment.

It's time to vote for Computational Design!

I wouldn't do this if it wasn't for a good cause...

Please, everyone who is interested in computational design and model based workflows, help to make this project reach the next stage: follow the link at the end of this page, subscribe and follow that project, propose 5 questions you would like to see on that stack exchange (look at mine for example, those are not platform related, I kindly ask you to do the same) and vote for questions proposed by others.

The goal now is to hit a minimum of 60 followers and 40 questions with 10 votes each so please don't waste your votes and thank you!

http://area51.stackexchange.com/proposals/97710/computational-design

Dynamo for pattern design

Recently I have been asked to demonstrate how Dynamo can help in the manufacturing market, especially in pattern generation, so I came up with this little example that can show all core Dynamo features at once: the Visual Scripting side by side with some Dynamo Script as well as some Python Nodes, Complex Geometry controlled by Parameters, Pattern generation, Lists handling, the Connection with External Resources (in this case Images) that can be used to generate information, the Export to SAT format to bring the idea in the physical world through other platforms such as Fusion 360.

If you were looking for a tool that does right that, you've found it, but Dynamo is much more!

New Autodesk Blog around BIM and Beyond

Behold everyone, there is a brand new blog around BIM and cool stuff like Dynamo and React Structures that you might want to keep an eye on, so please subscribe and add it to your favorite readings, let's see what's in the box!

Delaunay Triangulation with Dynamo

I was reading a tweet by Dimitar Venkov and it caught my attention, how can you use Dynamo to create a triangular mesh from a list of points, here is the discussion on the forum.

I was looking at the same problem my self not too long ago, it is achievable in Dynamo too but there is a lot to learn about Delaunay Triangulation and the algorithms to solve it.

Searching on the internet I've found several examples, the one I decided to try to implement in Dynamo is this one.

Basically is what Revit does when it reads a LandXML file and converts it into a Topographic Surface, well... almost..., therefore some "ghost" triangles outside the true mesh are going to appear.

If it is possible to add an outline, like a polycurve, they could be removed with a little bit extra effort.

This is not yet a Constrained Delaunay Triangulation though, but it works.

To be honest I had to swap the Y and Z coordinates in this example ant then swap it back before creating the surfaces and get rid of an extra "construction" triangle in the latest while loop.

Using the same algorithm it is possible to derive the IndexGroups  and create a Dynamo Mesh from the same list of points, the graphical result is quite different and smooth.

Once again our Dynamo Swiss Knife saved the day.

BIM Manager / BIM Coordinator wanted

Maffeis Engineering S.p.a. based in Solagna (VI) is looking for a BIM Manager and a BIM Coordinator with a very good knowledge of Revit and the BIM workflows.

Please get in touch with the human resources to send a CV (English) and ask for more details about this position and job description (I don't retain anymore information unfortunately).